Qu'est-ce que la radioactivité ?

​Dans la nature, la plupart des noyaux d’atomes sont stables, c’est-à-dire qu’ils restent indéfiniment identiques à eux-mêmes.
Les autres sont instables car ils possèdent trop de protons ou de neutrons ou trop des deux.
Pour revenir vers un état stable, ils sont obligés de se transformer.
Ils expulsent alors de l’énergie -provenant de la modification du noyau – sous forme de rayonnements :
c’est le phénomène de radioactivité.

I.Stabilité et instabilité des noyaux

I.1- Composition d’un noyau et notation

a. Composition d’un noyau

b. Symbole d’un noyau

Le noyau d’un atome est noté sous la forme :

Remarques:

Rem. 1 :    Z est appelé nombre de charge ou numéro atomique pour un atome.




Rem. 1 :    A est appelé nombre de masse (la masse (en g) d’une mole de noyau est proche de la valeur de A).




I.2- Les isotopes

Des noyaux isotopes sont des noyaux possédant même nombre de protons Z (ils appartiennent donc au même élément chimique)
mais des nombres de nucléons A différents (ils ne différent que par leur nombre de neutrons)



Rem. :    il existe 90 éléments chimiques naturels et 350 nucléides naturels (on parle de nucléide pour des noyaux strictement identiques :
même nombre de protons et de neutrons). On connait environ 1500 nucléides




Exemple :



I.3- Les noyaux radioactifs


 

Les deux nucléides carbone 12 et carbone 14, bien qu’isotopes, ne possèdent pas les mêmes propriétés.
En effet le carbone 12 est un nucléide stable alors que le carbone 14 est un nucléide instable (on parle alors de radionucléide)
: il peut se désintégrer spontanément pour se transformer en un autre noyau. Lors de sa désintégration, il émet une particule.



Un noyau radioactif est un isotope instable d’un élément chimique. Il va naturellement se désintégrer pour chercher
à atteindre une composition stable. Lors de la désintégration, le noyau radioactif émet une particule et de l’énergie.

I.4- Diagramme de Segré -carte (N,Z)

Le diagramme (Z; N) représente l’ensemble des noyaux connus en fonction de leur numéro atomique Z en abscisse et de leur nombre de neutrons N en ordonnée (ou l’inverse).
Un code couleur permet de différencier les noyaux stables des noyaux instables. :

Il existe deux types de noyaux: Noyaux stables :conservent toujours la même structure Noyaux instables : ou noyaux radioactifs se transforment spontanément à d’autres noyaux avec émission de rayonnement. Sur le document ci-contre, sont reportés les noyaux avec en abscisse le numéro atomique Z et en ordonné le nombre de neutrons N1. Les nucléides stables sont en rouge et occupent la partie centrale appelée vallée de stabilité. Jusqu’à Z = 20, les nucléides stables se situent au voisinage de la droite N = Z : ils possèdent autant de protons que de neutrons. Pour Z < 20 les noyaux stables se situent au voisinage de la droite N=Z . Leurs nombres de neutrons et de protons sont donc égaux Aucun noyau dont Z>82 n’est stable.




Les noyaux  radioactifs se désintègrent en se rapprochant de la courbe de stabilité après l’émission de rayonnements radioactifs énergétiques :

• Les noyaux dont le nombre de protons est trop grand sont du type émetteur bêta plus (β⁺)
• Les noyaux dont Z est trop faible sont du type émetteur bêta moins (β^–)
• Les noyaux lourds avec un excès de protons sont des émetteurs alpha (α)

II.La radioactivité

II.1- Définitions de la radioactivité

Un noyau radioactif est un noyau instable qui se désintègre spontanément en émettant une particule.

La radioactivité est une désintégration naturelle d’un noyau radioactif à un noyau fils plus stable avec émission d’une particule.




II.2- Propriétés de la radioactivité

• La désintégration radioactive est un phénomène :

• Aléatoire : la date à laquelle intervient la désintégration d’un noyau est imprévisible ;     

• Spontané : elle se déclenche seule, sans intervention extérieure ; indépendant de  la température, de la pression,….

• inéluctable : un noyau radioactif finit forcément par se désintégrer;     

II.3- Lois de conservation

Les transformations nucléaires obéissent à des lois de conservation, appelées lois de conservation de Soddy : Au cours  des transformations nucléaires, il y a conservation du nombre de charge Z et du nombre de nucléons A.

Les transformations nucléaires obéissent à des lois de conservation, appelées lois de conservation de Soddy :
Au cours  des transformations nucléaires, il y a conservation du nombre de charge Z et du nombre de nucléons A.



• Un noyau père (X) donne naissance à un noyau fils (Y) en émettant une particule P  chargée :


Au cours de cette réaction nucléaire, il y a conservation :

    (1)    Du nombre de masse : A = A’ + a
    (2)    Du nombre de charge : Z = Z’ + z

II.4- Les différents types d’émissions radioactives


   

• alpha α : la particule est un noyau d’hélium  ₂⁴He
• bêta moins β^– : la particule émise est un électron _-1e
• bêta plus β⁺ : la particule est un positron  ₊₁e
Remarque:   
• Les rayons X  se comparent aux rayons gamma et sont essentiellement produits par des moyens artificiels plutôt que par des substances radioactives.

Les équations de la radioactivité

a.la Radioactivité α

- Un noyau lourd instable éjecte une particule α et donne un noyau fils plus léger, généralement dans un état excité

l’équation de la réaction.

   



b.la Radioactivité β –

Cette radioactivité se manifeste lorsque le noyau présente un excès de neutrons.

- Au cours de la désintégration, il y a émission : D’un électron noté β^- .

l’équation de la réaction.

   



c.La radioactivité β +

Cette radioactivité se manifeste lorsque le noyau d’un atome possède trop de protons. - Au cours de la désintégration, il y a émission : d’un positon noté β⁺ .

l’équation de la réaction.

   



d. La désexcitation γ

Le noyau-fils est le plus souvent dans un état instable, il libère son excédant d’énergie sous forme de rayonnement γ, il se désexcite..




l’équation de la réaction.

   

Exercice d'application  : Utiliser les lois de conservation.

Énoncé Utiliser les lois de conservation Recopier et compléter les équations des réactions nucléaires en déterminant les valeurs de A et de Z : a.    b.    c.   Identifier la particule "P" et donner son symbole.

III.Loi de décroissance radioactive

La radioactivité est un phénomène aléatoire spontané, imprévisible dans le temps  . L’évolution dans le temps d’un échantillon radioactif est soumise à une loi statistique appelée loi de décroissance radioactive (découvert par Rutherford et Soddy en 1902).

III.1- Loi de décroissance radioactive

Soit N le nombre de noyaux radioactifs initialement présents (à l’instant t=0)

Soit N(t)  le nombre de noyaux radioactifs présents à un instant t quelconque restants (non désintégrés).

le nombre de noyaux diminue au cours du temps donc  à l’instant   t+dt :

N_t+dt – N_t = dN(t) <0  ) donc   (– dN(t)>0)  nombre de noyaux radioactifs disparus   (désintégrés)  pendant une durée très brève dt 

Les expériences ont confirmé que −dN(t)est proportionnelle à N(t) et dt.

C-à-d     – dN(t)= λ.N(t).dt    en fin   dN(t) = −λ × N(t) × dt

La résolution de cette équation donne         N(t)= N₀e ^−λ×t

λ est la constante radioactive, qui  dépend de la nature du noyau radioactif,représente la proportion de noyaux qui se désintègre par unité de temps  elle s’exprime en s^-1 .

Note : λ= Landa = Constante radioactive

N.B : La démonstration de cette expression mathématique n’est pas à connaître pour l’épreuve de physique au terminal.

  

Par conséquent, nous exprimons la loi de décroissance radioactive d’un échantillon radioactif comme suit : A l’instant  t   on a :  N(t)= N₀e ^−λ×t

Avec

• N₀ le nombre de noyaux initialement présents dans l’échantillon
• N(t)  le nombre de noyaux radioactifs  encore présents à l’instant
• λ représente la constante radioactive en s^-1 , propre au corps considéré

III.2- Constante de temps et demi-vie ( la période T)

On définit la constante de temps notée τ exprimée s en (SI)   
par l'expression :     :     τ = 1 / λ



Cette constante de temps est caractéristique de la désintégration 

La demi-vie t1/2 d’un échantillon de noyaux radioactifs est la durée au bout de laquelle la moitié des noyaux initialement présents se sont désintégrés.

selon l'expression de la loi de la decroissance-radioactive :           N(t)= N₀e ^−λ×t        
à la date                





   

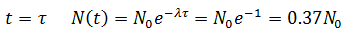
Au bout d'un temps de demi-vie     

t_1/2 l'équation s'écrit :     


La demi-vie est une constante caractéristique d’un élément radioactif.

III.4- Activité d’un échantillon radioactif

  Définition :  

L’activité A(t)  A(t)  ,(ou a(t)) , d’un échantillon contenant un nombre N(t) d’atomes radioactifs, correspond au nombre de désintégrations par seconde ayant lieu au sein de cet échantillon. L’activité s’exprime en becquerels (Bq = s^-1 ), et représente l’opposé de la dérivée par rapport au temps du nombre d’atomes radioactifs restant dans l’échantillon à un instant t :   
 
A(t)=	-dN(t)
	dt



Remarque :

On a pu établir que la constante de conversion de l’activité exprimée en nombre de désintégrations par seconde (becquerels) a pour valeur :

$$1\mathrm{C}\mathrm{i}=3,7\times <!--\; \times \; -->{10}^{10}\mathrm{B}\mathrm{q}$$

 Évolution de l’activité



puisque d'après la definition de l'activité on a :

 

A(t)=	-dN(t)
	dt

et d'après l'expression de la loi de décroissance radioactive ona : N(t)= N₀e ^−λ×t  

alors :
 

A(t)=	-dN0e −λ×t	=  λN0e −λ×t
	dt

 

 On retrouve finalement l’expression de l’activité à l'instant  t  :        

 

A(t)=	-dN(t)	=  λN(t)
	dt

   En posant   à (t=0)  :  l'activité initiale A(t=0) s'écrit  :  A₀ =λ×N₀




III.5- Application : Datation radioactive

  

Comment procède-t-on pour la datation ?

Dans l’atmosphère, les particules (neutrons) cosmiques entrent en collision avec des atomes d’azote. Au cours  de ce choc, l’atome d’azote perd un proton et se transforme en carbone 14.



Le carbone radioactif se lie avec de l’oxygène pour former du dioxyde de carbone qui est  échangé  avec le monde vivant  (respiration par les plantes, grâce à la photosynthèse, alimentation et  respiration des organismes vivants. Aussi longtemps qu’un organisme vivants vit encore, il  continue de prélever du Carbone 14, dont la proportion reste fixe : 

(1 atome de Carbone 14 pour 750 milliards d’atomes de Carbone 12)

• Pendant toute leur vie, la proportion de carbone 14 reste constante.
• Dès qu’un organisme meurt, le carbone 14 qu’il contient n’est plus renouvelé puisque les échanges avec le monde extérieur cessent, sa proportion se met à décroître  selon l’équation  :



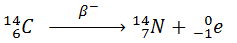
On mesure l’activité a(t) d’une masse d’échantillon connue, et connaître a l’activité de la même masse d’un échantillon témoin existant. Alors, on peut déterminer son âge t par la relation suivante :



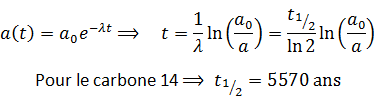
Exercice d'Application

Le ${}^{14}C$disparaît progressivement de la matière organique à partir de sa mort. Exemple connu : fragments de tissu de lin trouvés dans un habitat préhistorique. Par combustion, on a obtenu du CO2 une activité de 241 désintégrations par heure et par litre. Avec un tissu similaire, fabriqué de nos jours, l’activité est de 492. On sait que le ${}^{14}C$ a une période de 5730 ans.
On applique la loi de désintégration :

$$\begin{array}{rl}N& =N_0\exp <!--\; \; -->(-<!--\; -\; -->\mathrm{\lambda <!--\; \lambda \; -->}t)=N_0\exp <!--\; \; -->(-<!--\; -\; -->\frac{t}{T}\ln <!--\; \; -->2)\\ \ln <!--\; \; -->(\frac{N_0}{N})& =\frac{t}{T}\ln <!--\; \; -->2\end{array}$$

En tenant compte que l’activité d’un échantillon est proportionnelle au nombre d’atomes qu’il contient :

$$\begin{array}{rl}\frac{A_0}{A}& =\frac{N_0}{N}\\ t& =T\frac{\ln <!--\; \; -->(A_0/A)}{\ln <!--\; \; -->2}=5730\frac{\ln <!--\; \; -->(492/241)}{\ln <!--\; \; -->(2)}=5900\text{ans}\end{array}$$